Optimization and uncertainty quantification model for time-continuous geothermal energy extraction undergoing re-injection
Abstract
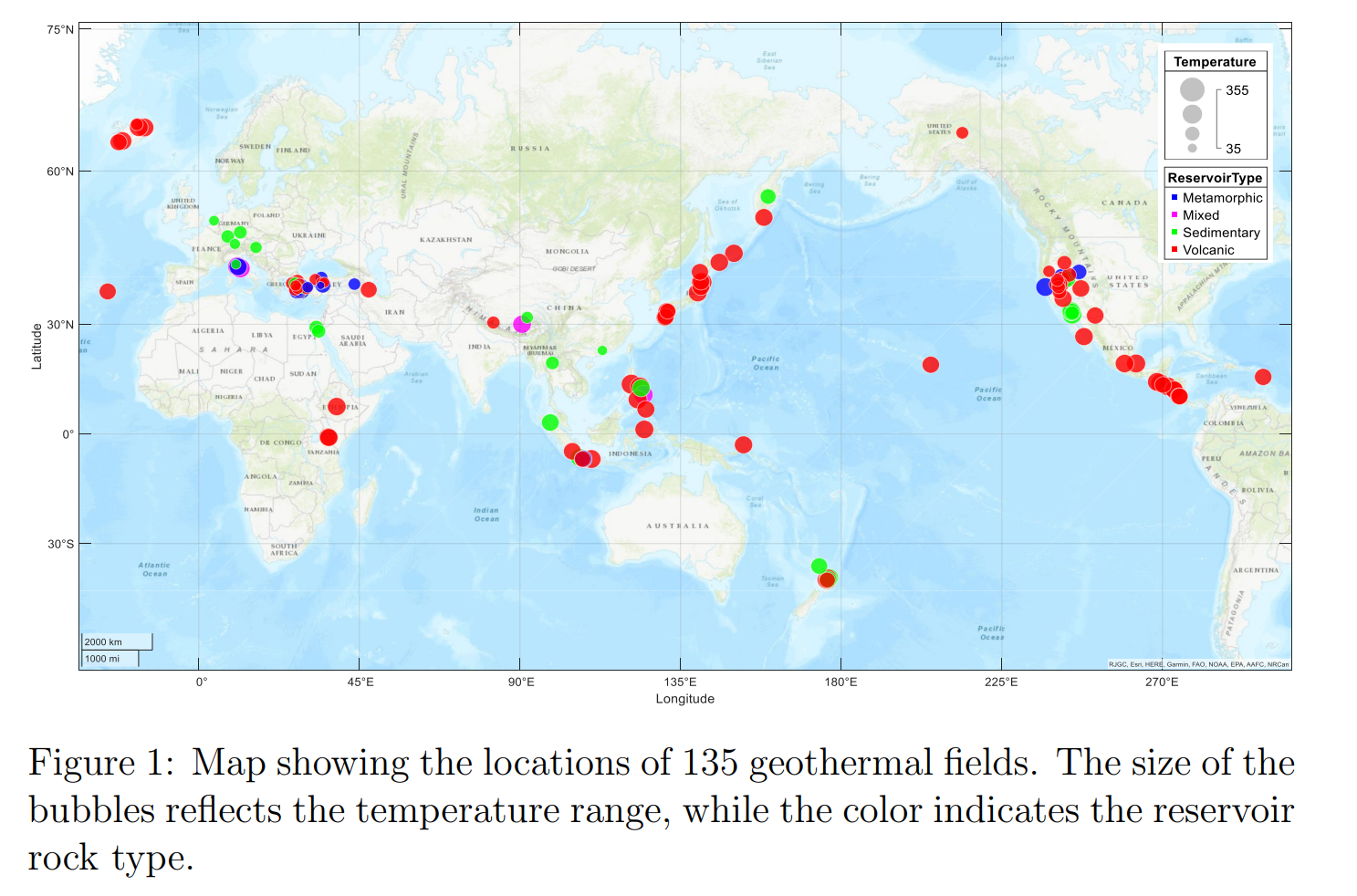
- 地热田模拟通常与地下静态物性、流体流动和传热动力学相关的不确定性相关。使用模拟进行不确定性量化是设计最佳地热田开发方案和指导决策的有用工具。优化过程包括对多个时间相关流动机制的评估,这些机制是受地下不确定性影响的操作参数的函数。此过程需要仔细确定参数范围、相关性及其概率分布函数。本研究提出了一种新的方法来评估采热和生成焓率的时间相关预测,包括不确定性量化和优化。将时间连续和多目标不确定性量化用于地热开采,和水回注方案。操作参数和不确定性参数的范围是根据收集的数据库确定的,其中包括全球135个地热田。
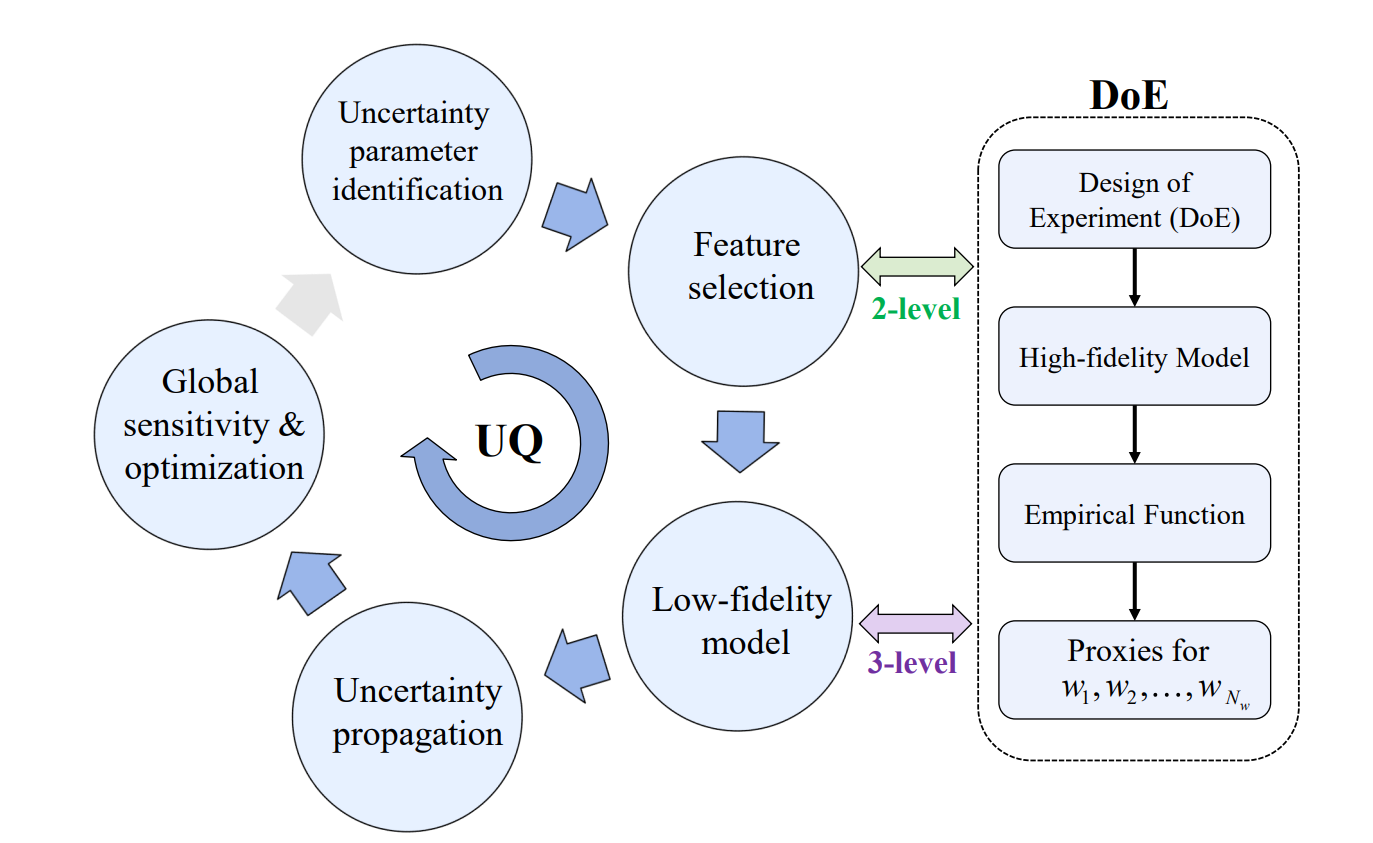
- 基于将低保真度模型与蒙特卡罗分析相结合的工作流程,以无干扰方式进行不确定性计算。全物理油藏模拟用于构建和验证低保真度模型。采样过程通过实验方案设计,空间填充增强,并结合协方差分析来捕获参数相关性。然后,根据无量纲群,将预测的采热率和生成焓率作为重要不确定性参数的函数进行评估。该工作流程适用于各种地热田,以评估其井配置中的最佳井距。该方法为用于地热场模拟和优化的时间连续不确定性量化和全局敏感性分析提供了有效且稳健的工作流程。
- Geothermal field modeling is often associated with uncertainties related to the subsurface static properties and the dynamics of fluid flow and heat transfer. Uncertainty quantification using simulations is a useful tool to design optimum field-development alternatives and to guide decision-making. The optimization process includes assessments of multiple time-dependent flow mechanisms, which are functions of operational parameters subject to subsurface uncertainties. This process requires careful determination of the parameter ranges, dependencies, and their probabilistic distribution functions. This study presents a new approach to assess time-dependent predictions of thermal recovery and produced-enthalpy rates, including uncertainty quantification and optimization. We use time-continuous and multi-objective uncertainty quantification for geothermal recovery, undergoing a water re-injection scheme. The ranges of operational and uncertainty parameters are determined from a collected database, including 135 geothermal fields worldwide.
- The uncertainty calculation is conducted non-intrusively, based on a workflow that couples low-fidelity models with Monte Carlo analysis. Full-physics reservoir simulations are used to construct and verify the low-fidelity models. The sampling process is performed with Design of Experiments, enhanced with space-filling, and combined with analysis of covariance to capture parameter dependencies. The predicted thermal recovery and produced-enthalpy rates are then evaluated as functions of the significant uncertainty parameters based on dimensionless groups. The workflow is applied for various geothermal fields to assess their optimum well-spacing in their well configuration. This approach offers an efficient and robust workflow for time-continuous uncertainty quantification and global sensitivity analysis applied for geothermal field modeling and optimization.
Keywords:
Geothermal reservoirs, Uncertainty quantification, Design of Experiments, time-dependent Optimization, Proxy modeling